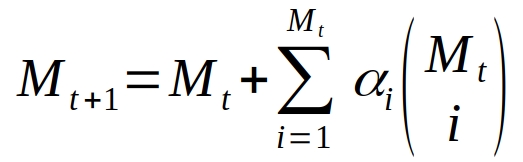Theory of the Adjacent Possible

Posted on

The very first tools used by humans (or rather, their evolutionary ancestors) consisted of items that were found in the environment, such as stones, sticks, and bones. Now, millions of years later, we have an endless range of sophisticated technologies, from paperclips, multi-tools, and conveyor belts, to trains, computers, and the international space station. So how did we get from a handful of primitive tools to these countless advanced technologies? One possible answer to this question about technological evolution is provided by the Theory of the Adjacent Possible, or simply called TAP.

Hockey stick growth

It is well known that the economy shows a growth pattern resembling a hockey stick. For a long time there was steady but very slow growth. Then, around the time of the industrial revolution, the economy suddenly started growing faster, and has grown increasingly fast ever since.

A standard proxy for measuring economic growth is gross domestic product (GDP) over time. The graph below shows (estimated) world GDP over the last two millennia. It clearly shows the three stages of slow but steady growth, initial increase in growth rate, and then shooting up very fast.

Combinatorial innovation

This economic growth is largely driven by technological innovation. And technology, in turn, is largely combinatorial in nature. New technology often consists of innovative and improved combinations of currently existing technology. This holds for the very first tools used millions of years ago as well as technology from the industrial revolution and beyond.

For example, once early humans (or their ancestors) had discovered how to use stones and sticks as tools, the first truly innovative technology consisted of combinations of these, such as a stone axe. Combining a stone that was already used as a hand axe, a stick, and some string (perhaps in the form of dried grass or other plants), a stone axe was made by stringing the hand axe to a strong stick.

With modern technology it is not always directly obvious anymore what the earlier technologies were that combined to make a new technology. However, going back to the very first versions of such modern technology can reveal this more clearly. For example, the earliest trains were a combination of a (steam) locomotive as was already used in, for example, coal mines, and carriages that were originally drawn by horses.

The image below shows a beautiful example of this. It is a painting by the American artist Edward Henry called “The First Railroad Train on the Mohawk and Hudson Road“. If you click on the image for a larger view, you can clearly see that the train carriages were still exactly the same as the ones originally drawn by horses (such as the ones on the left in the painting), simply put on rails. In fact, some of the passengers were even still sitting on the outside of the carriages!

Theory of the adjacent possible

When there are only a few current technologies, or tools, there are also relatively few possible combinations to create new technology. However, when the number of existing technologies increases, the number of possible combinations increases even faster. Of course not all of these new combinations might be useful in any way, but even if just a small fraction of them are, there is an ever expanding space of possibilities for new inventions and innovations over time.

This is what the theory of the adjacent possible (TAP), as proposed by Stuart Kauffman, is all about. At any moment there is an “adjacent possible” of all the potential new combinations of currently existing technologies, and with every actual innovation this adjacent possible grows larger, giving rise to even more (potential) new combinations. Millions of years ago, trains were not in the adjacent possible yet, but stone axes were. The invention of the steam engine increased the adjacent possible very significantly, which then also included locomotives and, subsequently, trains.

This core idea is captured mathematically in the TAP equation:

Here, \(M_t\) is the number of “technologies” (i.e., types of tools, goods, items, etc.) in existence at a given time \(t\). The parameters \(\alpha_i\) are a series of increasingly small probabilities indicating, for example, the probability that a given combination of \(i\) existing items forms a useful new tool or technology. Finally, the expression \({M_t \choose i}\) stands for the number of ways in which one can choose \(i\) items out of a total of \(M_t\). (Note that this equation actually generates non-integer values for \(M_t\), but this can be easily taken care of in practice, for example by rounding the value at each time step; this will not change the overall behavior.)

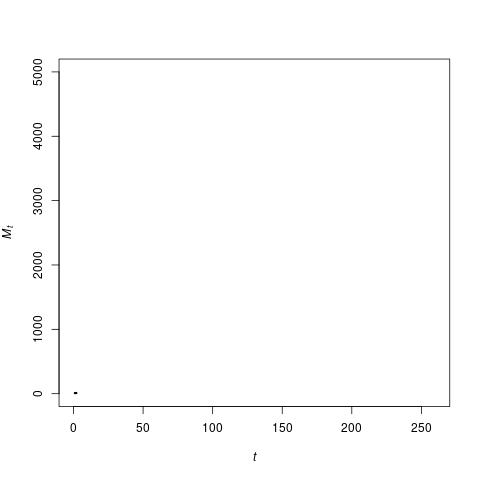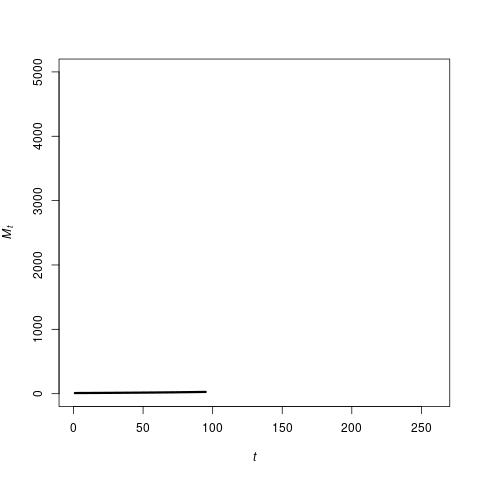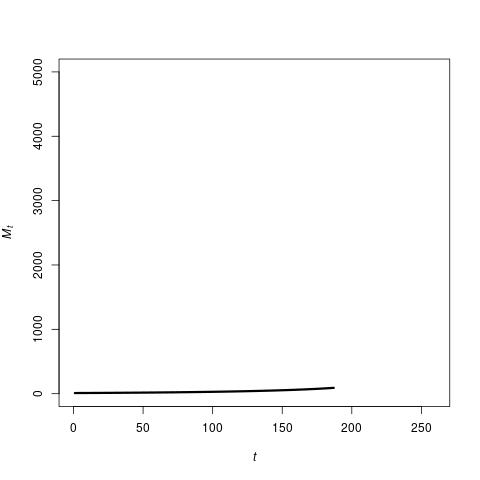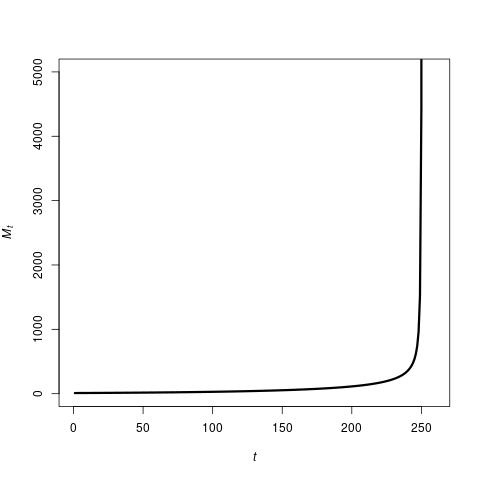
In short, the TAP equation gives a mathematical expression for how the number of “items” \(M_t\) in an economy grows when new types of items are created from combinations of 1, 2, 3, 4, or any number \(i\) of currently existing items, and given a certain probability of “success” for such new items (with decreasing probabilities for combinations of a larger number of existing items). This TAP equation accurately reproduces the hockey stick growth of the real economy, as the image below shows (note, though, that because of the choice of parameter values, the scales are different from the GDP graph above).

TAP thus provides a simple but mathematically precise explanation for technological evolution and economic growth in terms of combinatorial innovation. This fundamental equation also reproduces other phenomena in economics and elsewhere, and would suggest an inevitability to the anthropocene. However, those topics are beyond the scope of this general introduction, but here are some (more technical) references for further reading/listening:

If you cannot get the full article through the publisher’s website for some of these references, you can download a free preprint from my list of publications (just click on the PDF icon next to the relevant article title in that list).